Electricity for Synth-DIY'ers: Operational Amplifiers

Now that we've covered the basic semiconductors and passive components, let's begin covering what happens when you put a bunch of them together on a slab of silicon -- the integrated circuit. One of the most basic integrated circuits, used in both analog and digital systems, is the operational amplifier, or op amp for short. Op amps are one of the most useful ICs; they can be used to amplify or attenuate a signal to any extent desired, invert a signal, and solve signal buffering and impedence-matching problems. Further, they can be used to conveniently implement active filters in the audio range, do voltage level comparisons, and a host of other analog signal processing functions.

The development of the operational amplifier actually precedes the advent of the integrated circuit. Op amps were first devised in the 1930s as a means of solving various amplification and impedence-matching problems in long line telephone circuits. At the time, they were obviously constructed using tubes since the transistor had not yet been invented; as the circuits were mass produced, they started being packaged into forms that allowed them to be treated as a single component -- some tube types were packaged such that the entire circuit could be plugged into a socket as if it were a single tube.



Philbrick Labs K2-W tube-based operational amplifier. Photo from Wikipedia Commons.

Much research in the pre-IC days went into miniaturizing these circuits, and making them work at lower voltages. A few op amps intended for high-end audio applications are still made as "bricks" implemented with discrete transistors, but nearly all other types are made as ICs these days. (An aside: One engineer who played a significant role in the development of the early solid-state op amps was a certain young Alan R. Pearlman, who would later play a much larger role in the development of the music synthesizer.)

The first monolithic IC op amps were developed by Fairchild in the early 1960s. They introduced the first one, the µA702, in 1963; it had some unfortunate characteristics and was not a success. However, in 1965 they followed this up with the µA709, which fixed the 702's problems and went on to see widespread use; it remained in production into the 1980s. Then things picked up; National Semiconductor challenged Fairchild by introducing its LM101/201/301 series in 1967. (The series of numbers represented different ambient operating temperature ranges, with the 3xx being the commercial series and the 1xx being mil-spec; this pattern continues today for most ICs designed by National.) Fairchild said "oh, yeah?" and the next year they introduced what would become the canonical op amp for decades: the µA741. The 741 was the first internally-compensated op amp (we'll get to compensation later). Variants of the 741 are still in production today.

If you are interested in reading a very good and detailed story of the development of the op amp, see this paper published by Analog Devices.

Opamp Basics

A basic opamp has two inputs and one output. The two inputs are known as the inverting and non-inverting inputs; as one might guess, the output will be inversely proportional to the signal at the inverting input, and directly proportional to the signal at the non-inverting input. That's a bit of an over-simplification, though; it often leads beginners to believe that what the opamp does is amplify the difference between the two inputs. There's more to how an opamp works than that, though.

Here, in three short rules, is what an opamp does (or tries to do):

1. The opamp wants the voltage at its two inputs to be equal.
2. It assumes that a feedback path exists between the output and the inverting input.
3. It uses this assumption to vary the output to try to make the two inputs equal.

If no feedback path exists, the opamp will drive its output to its minimum or maximum voltage, which depends on the power supply voltages and the opamp's circuit design. (Some opamps will go "to the rails" and some will stop a volt or two short.) Thus, most useful opamp circuits include a negative feedback path. Another way of putting this is that without any feedback, the opamp has extremely high gain -- almost any non-zero inputs drive it to clipping, in one direction or the other. (The theoretical ideal opamp has infinite open-loop gain. Real opamps of course cannot go to infinity, but most types have open-loop gain factors within the audio range in the tens of thousands.) The feedback path is what controls this gain. From there, it follows that how much feedback is supplied can control the opamp to provide more or less gain, and this is exactly the case.

Symbology

We'll introduce the symbology at this point. The symbol for a basic opamp is:

The two pins show on the left are the two inputs: inverting (indicated by '-') and non-inverting (indicated by '+'). The pin on the right is the output. The power and ground pins are frequently not show, but when they are, they are show sticking out of the top and bottom; any other special-purpose inputs that the op amp has will also be shown at the top or bottom. In isolation, illustrators will usually draw the opamp symbol with the non-inverting input above the inverting input. However, in a schematic, the reverse is often true; conventionally the feedback path is drawn above the opamp symbol, and since it connects to the inverting input, to reduce the number of crossing paths the inverting input frequently gets placed on top. Some schematics will use the '+' symbol to indicate the non-inverting input and the '-' symbol to indicate the inverting. But others will use the pin numbers of the specific IC, in which case you need to know what kind of opamp it is and have access to the pinout. In this article, we will keep the non-inverting input on top throughout, to reduce confusion.

The Basic Amplifier Circuits

There are two basic configurations of amplifier circuits using an opamp, the inverting configuration and the non-inverting configuration. The inverting configuration has the effect of the output being the inverse of the input; with the non-inverting configuration, the output is identical to the input except for gain. Although the inverting configuration is used more, the non-inverting configuration is easier to understand and it does have its uses, so we'll introduce it first. It looks like this:

Note the resistor connected between the output and the inverting input. This is the feedback path. Thinking back to the three rules, picture what happens when a positive voltage comes to the opamp from the external circuitry. It raises the voltage at the non-inverting input. The opamp then wants the inverting input to rise to the same voltage as the non-inverting input. In order to accomplish this, it raises the voltage level at the output.

That voltage goes over to the inverting input, where some of it is bled off to ground by the other resistor. The two resistors form a voltage divider, so the voltage at the inverting input will be some fraction of the voltage at the output. Therefore, the output voltage will have to go up higher than the voltage present at the non-inverting input before the voltages at the two inputs become equal. For instance, if the two resistors have the same value, then they form a divide-by-2 divider, and the output will have to rise to twice the voltage that is present at the non-inverting input before the circuit settles.

All of this happens very fast. The speed at which the opamp is capable of responding to its input determines its maximum response frequency, or bandwidth. Nearly every opamp on the market today has a bandwidth that extends well beyond the audio range, so in an audio application, you will rarely have to worry about it; you can assume that everything happens instantaneously. (If you get into radio, or high-speed data circuits, that assumption is no longer valid.)

The ratio of the two resistors determines the gain of this circuit. The ratio in the middle of a two-resistor voltage divider is the total resistance divided by the resistance of the "bottom" resistor; in this case R2. So the gain of the non-inverting amplifier configuration is (R1+R2)/R2, or (R1/R2)+1. In the simplest case, where R1 is replaced by a straight wire (i.e., zero resistance) and R2 is omitted (infinite resistance), the result is a unity-gain amplifier; the output will be identical to the input. What good is a unity-gain amplifier? Well, one use is for re-driving signals that can't take being loaded down, such as signals from guitar pickups. Many opamps have extremely high input impedance, and a unity gain buffer is perfect for taking signals from high-impedance sources and repeating them with lower output impedance. Note one implication of the gain formula: in the non-inverting configuration, you can't achieve a gain of less than 1.

(By the way, in practical circuits, it's not a good idea to totally omit R2. Opamps often "bleed" a very small amount of current internally back into their inputs. If this bleed current doesn't have a path to ground, it can cause the opamp to go open loop and drive the output to the rail. If the need is for a unity-gain circuit, a 1M resistor can usually be used for R2 without any practical effect on the gain ratio, and it will allow the leakage currents to bleed off.)

The inverting amplifier configuration looks like this:

How does this one work? Per the three rules, when a positive voltage comes from the external circuit, it applies a positive voltage to the inverting input. Because it is the inverting input, the opamp will respond by pushing the output negative, in an attempt to counterbalance the positive voltage and bring it back to the voltage level of the non-inverting input, which is at 0V since it's grounded. The voltage level that the output has to go to in order to accomplish this depends on the ratio of the two resistors. Since the resistors directly determine the proportion of the input signal and the feedback that get combined at the inverting input, the gain equation for the inverting configuration is simply R1/R2. Unlike the non-inverting configuration, the inverting configuration can achieve a gain of less than 1; as you can see from the formula, as R2 gets large, the gain goes towards zero. Thus the inverting configuration can be both an amplifier and an attenuator.

So when do you choose one configuration over the other? Well, for one thing, the inverting configuration obviously inverts the signal, which is useful in its own right sometimes. More importantly, though, is that you will see below that most of the more sophisticated op amp circuits require an inverting configuration -- they don't work the other way. So why not just use the inverting configuration for everything? Well, for one thing, this may result in unintended inversion of the input, which will make you have to add an extra inverting stage to get the signal right side up.

However, a more important reason is in the fact that, in the inverting configuration, the two gain-setting resistors provide a "sneak path" around the op amp between the input and the output. This can cause a problem regarding the input impedance of the circuit. The op amp itself has incredibly high input impedance, which can be a very useful property (in, e.g., a preamp for a mic or guitar). However, if the op amp is driving something else with low input impedance, the path through the resistors will lower the effective input impedance. You could fix that by using high values for both resistors, since the ratio of the resistors and not the values per se is what determines the gain. However, past a certain point (when one of the resistors gets up past about 100K), you will start to have noise and voltage offset problems.

The non-inverting configuration does not have this problem because there is no connection between the input and the feedback path. So what you often see is that, for a given device, non-inverting circuits are often used for the external inputs and outputs, and most everything in between uses inverting circuits.

Stuff You Need to Know at This Point

Now that you understand the basic principles behind the opamp, before we proceed let's go over some of the requirements and practical limits of real opamps. Most opamps require both a positive and a negative power supply, depending on the type, and these must usually be of the same magnitude in order for the opamp to work properly. In other words, if the negative supply is -15V, a positive supply of +5V won't do; you need +15V. The power supply voltages limit how far the output can swing in either direction. They also limit what input voltages are permitted; with most opamp types, the inputs must be kept at least 1-2V away from the supply voltages. If the input limits are exceeded, the opamp may go into a condition called "latchup" where it no longer responds to its inputs. Latchup generally requires that the power be removed to reset the circuit, and it may harm the IC. If there is a possibility of the inputs exceeding the opamp's specified voltage, such as an opamp connected to an external input jack, it is a good idea to protect the inputs. Usually this is done with zener diodes. There are opamps which can accept input voltages all the way to the supply voltages; check the vendor catalogs if you need one of these.

There are some opamps made to work with single supply voltages. These are sometimes useful particularly in battery-powered applications. With these, the input voltages must be kept between the power supply voltage and ground, so if you want to feed in an AC signal, you will need to add DC offset to the input and then remove it from the output.

Most modern opamps are protected against having their outputs short-circuited; if you short the output to ground, nothing bad will happen. However, there is a limit to how much current the output can supply, so if you short it to ground, the output will go to zero and stay there until you remove the short. The output current limits are printed in the specifications. If you are building a circuit to drive a very long cable -- say, an output module for a modular that needs to drive to the house mixer 75 feet away -- an opamp will a high-current output capability will be useful.

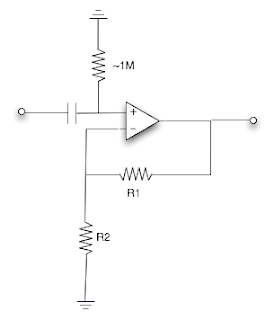
One other thing to be aware of: All op amps "leak" very small amount bias currents that occur internally on the inputs. These small currents have to have a path out via the input pins. Here's something to watch out for:

Note the capacitor on the non-inverting input; this would be typical if it was desired to block DC voltages from reaching the input. The problem is: those micro-leakages at the input are "trapped" by the capacitor; they don't have a path out of the circuit! The result is that the circuit will never reach equilibrium and the output will probably go to the minimum or maximum voltage and stay there. Here's how you fix that:

The extra resistor allows the leakage currents to bleed to ground. A 1M resistor will usually be large enough to not have any effect on the input signal.

Analog Arithmetic with Opamps

A frequent problem in synth circuits is the need to add or subtract control voltages. For instance, the control voltage fed to a VCO might need to be the sum of control voltages from the keyboard, the pitch wheel, and an LFO. Here is a circuit that will sum up any number of control voltages:



You can add any number of inputs to the input ladder at the left. To keep things simple, all of the Rx resistors should be of the same value; if you do so, the gain is Ry/Rx. Use Rx values of at least 1K to prevent the input signals from trying to back-drive each other. Note that, because this is based on the inverting-amplifier configuration, the output will be the negative of the sum of the inputs. That's easy to fix; just run it through a second inverting amplifier, with the gain configured as needed. Note that this circuit can also be used as an audio mixer; after all, a mixer is really just an adder. The one thing you might want to do if it is being used for audio mixing is add a DC-blocking capacitor (10 uF or so, non-polarized electrolytic) in series with each input.

You can subtract signals using the configuration above, preceded by an inverting amp that inverts the signal to be subtracted. However, here's a one-op-amp solution for computing the difference of two signals:



Note that this circuit is identical to what is commonly called a "difference amplifier" or "differential amplifier" (the latter is not-so-good terminology, but lots of people use it). The "balanced line" signal connection often used in recording studios consists of two signals, one of which is the negative of the other. You see this commonly in equipment such as microphones which use the 3-pin "Cannon" plugs and jacks; two of the pins carry the signals and the third is connected to the cable shield. You can use the difference amplifier circuit to convert this to a single-wire signal that you can process inside a piece of equipment. The difference amplifier produces an output which is proportional to the difference between its inputs. An interesting implication of this is that if both signals change by the same amount, the output does not change at all, because the difference between the signals didn't change. In the studio environment, this is called "common mode rejection" and is a big help in reducing noise pickup. The basic circuit should have R1 = R3 and R2 = R4; assuming so, then the gain is equal to R1/R2.

(Note that this is not the optimum version of this circuit; the main problem is that it's difficult to make the impedances of the two sides match exactly, which limits the circuit's accuracy. Here is an improved version, if you have a need for it.)

Differentiators and Integrators

Here's a pair of circuits that can be very useful particularly in a modular synth. The first is called a differentiator (not to be confused with a difference amplifier). What it does is produce an output which is proportional to the rate at which the input is changing; you can think of it as sort of a speedometer for the input signal. If the input is increasing, the output will be a positive voltage; if the input is decreasing, the output is negative, and if the input is not changing, the output is zero.



The gain of this circuit is proportional to the frequency of the signal fed into it, but is influenced by the values of R and C. The output voltage Vo = -RC(dV/dt), where R is the resistor value in ohms, C is the capacitor value in farads (not microfarads or nanofarads, but whole farads), and dV/dt is the rate at which the input voltage is rising or falling, in volts per second. (Don't worry about what the individual parts of the dV/dt stand for; just accept that it stands for "change in voltage with respect to time".) Note the minus sign, which is a result of this being an inverting-amp configuration. An easy way to think about this circuit is to assume an R of 1M and a C of 1 uF; this way the product of RC is 1, and then if the input is rising at 1V per second, the output is -1V as long as the input keeps changing.

The integrator is, mathematically, the opposite of the differentiator. To continue with the car analogy, you can think of the input as an accelerator for the output. When the input is positive, the output rises; its rate of rise is determined by the magnitude of the input. Same goes for a negative input; the output goes lower in proportion to the input. When the input is zero, the output remains where it was. Given that an input that remains positive or negative for any length of time will push the output to its power-supply-determined limit, it's useful to have a reset capability. This is shown in the schematic as a switch, but it would be a simple matter to substitute an NPN transistor or a mini relay so it could take a reset trigger signal.

Basic Active Filter Circuits

Consider the following circuit:



Note the capacitor in the feedback path. What is this capacitor doing to the feedback? Well, start by considering a very low frequency: At a low enough frequency, the capacitor is essentially an open circuit, so only the R1 resistor in parallel with it has any effect. This reduces to your basic inverting amplifier with gain determined by the formula for an inverting amplifier: R1/R2. But what happens as the frequency goes up: The capacitor starts to let some current through, in addition to what goes through R1. In effect, the capacitor is reducing the value of R1 by allowing some current to bypass it. This gets more pronounced as the frequency goes up, until the frequency is reached where the capacitor has effectively shorted out R1. At this point, R1's effective resistance is zero, and the full amount of feedback is being applied to the inverting input, which cancels out the input signal at that frequency and reduces the op amp's gain at that frequency.

This circuit is a low-pass filter. It has a certain gain at low frequencies and less gain as the frequency goes up; at a sufficiently high frequency, its gain is zero. Doing the math, we find that, just like any filter, there is a cutoff frequency determined by the capacitor's value and above that value the gain rolls off at 6 dB/octave, making it a single-pole filter. The cutoff frequency is: 1/(6.2832R1C) where R1 is in ohms and C is in whole farads.




This circuit is a high pass filter. From the above discussion, you can probably already guess how it works. At low frequencies, the capacitor is essentially open, so full feedback is applied to the inverting input, and the op amp's gain is zero. As the frequency increases, C starts to conduct and at a high enough frequency it essentially becomes a straight wire. At that frequency, the circuit's gain then is determined by R1/R2. The formula for cutoff frequency is the same as for the low pass filter. Note that this circuit, unlike the low pass filter circuit, is non-inverting with respect to the input. Inverting and non-inverting configurations exist for both low pass and high pass filters.

What if you want more than a one-pole response? Well, an obvious answer is to put several of the above circuits in series. For instance, if you use two, you get a two-pole filter with a 12 dB/octave rolloff. However, using this method for multi-pole filters means using an op amp for each stage, which can make for an expensive circuit. So, electrical engineers have devised all kinds of devious circuits for implementing multi-pole filters that do not need an op amp for each pole. For instance, the Sallen-Key circuit often used in synth filters implements a two-pole low pass or high pass filter with only one op amp.

Sallen-Key filter, from Wikipedia Commons

Op Amp Filter Topologies and Response Types

Here is something that people often get confused about when they read about op amp-based filter circuits. The topology is the logical arrangement of the components in the circuit. There are a bunch of ways of designing filter circuits, particularly multi-pole filter circuits. The Sallen-Key is one such topology; others often found in synths are the biquad and the multiple feedback. The response class refers to the general shape of the response curve. The three types you will hear most often in audio systems are Butterworth, Chebyshev, and Bessel; most synth filters belong to the Butterworth class. The differences between them are in exactly what the frequency response curve looks like; for instance, the Butterworth type is very flat in the passband, while the Chebyshev has some variations ("ripple"). All three of these filter types can be implemented in various topologies, and usually the difference is in the ratios between certain components. There is some pretty complicated math behind these, but you don't have to do the math; there are all kinds of design tools that allow you to plug in the desired characteristics and it will calculate the component values for you. Here is a simple one which will calculate a Sallen-Key (12 dB/octave) low-pass filter of the Butterworth class; all you have to put in is the desired cutoff frequency and one capacitor value. I'll do a future post which explains some of these active-filter types in more detail.

Compensation and Offset Nulling

All op amps require what is called compensation, in order to keep the op amp from going into self-oscillation under certain circuit conditions. The compensation consists of one or more capacitors that are placed into the op amp's internal circuitry. The first op amps were externally compensated -- they required the designer to add capacitors to compensation terminals on the device. However, most op amps today are internally compensated; the compensating capacitors are built into the op amp itself. In terms of ultimate performance, internally compensated op amps are a compromise; using external compensation allows the designer to extend the op amp's bandwidth and/or reduce its power draw, depending on the need. However, in designing synth circuits, these are seldom important factors. Therefore, there is usually no reason not to use internally compensated op amps in synth circuits.

The ideal op amp should, if both of its inputs are grounded, drive its output to exactly 0V. Real op amps will usually have an offset ranging from microvolts to a few millivolts, depending on how the inputs are configured. This is caused by small current leakages in or out of the input pins. Some op amps have inputs to which you can connect a trimmer pot that you can adjust to null out the offset. This can be important in, for instance, a control voltage input to a VCO. If you need this, look for an op amp type that has "balance" or "offset null" inputs.

Op Amp Types and Specifications

These days, nearly all op amps are packaged in the familiar dual-in-line plastic package, in either through-hole or surface mount configuration. (A very few of the oldest types are still available in the metal can that looks like an oversize transistor with more legs.) A single part often contains more than one actual op amp; dual, triple, and quad packages are common. Single types nearly always have 8 pins while types containing more than one per package may have up to 16 pins.

Things that you (maybe) need to be concerned about when you are searching for an op amp for a synth application are:

• Number of individual op amps in the package
• Minimum and maximum power supply voltages
• Input impedances
• The gain-bandwidth product
  
• Whether the op amp can run off of a single supply voltage
• The voltage range of the output
• Output drive capacity

We had a lot of fun back in the history writeup at the beginning of this article talking about the 741. However: Unless you are replacing a part in a vintage synth, don't even think about using one today. There are much better types available now. A popular general-purpose type is the TL08x series, originally designed by Texas Instruments but available now from multiple sources. These are available in various packaging containing 1, 2, or 4 individual op amps per unit. The inputs are JFET circuits and have very high input impedance. They can be powered at ±12V or 15V (the voltages used in modern modulars), and the permissible input voltages range to within 2V of the supply voltages. Another useful general-purpose type is the LM358, also available from multiple sources. It has most of the same virtues as the TL081 (single op amp per device); the input impedances aren't quite as high, but still adequate for most synth circuits. And they are inexpensive enough that you can buy a tube of 50 or so, to keep on hand for circuit prototyping or other off-the-cuff uses. Here is a table containing some potentially useful types that I extracted from the Mouser catalog. (The file is a .CSV file, which you can download and import into any spreadsheet application.)